µnos
TAYLORFORMEL
In der Analysis verwendet man die Taylor-Formel, um Funktionen in der Umgebung eines Punktes durch die sogenannten Taylor-Polynome anzunähern. Sie ist benannt nach dem Mathematiker Brook Taylor. Eng verwandt mit der Taylor-Formel ist die so genannte Taylorreihe.
Die Taylor-Formel ist aufgrund ihrer relativ einfachen Anwendbarkeit sowie Nützlichkeit Hilfsmittel in vielen Natur- und Ingenieurwissenschaften geworden.
1. Definition und Satz 2. Beweis 3. Restgliedformeln 4. Näherungsformeln für Sinus und Kosinus 5. Taylor-Formel im Mehrdimensionalen
1. Definition und Satz
Sei I ein reelles Intervall und 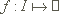 eine (n+1)-mal stetig differenzierbare Funktion. Dann gilt für alle a und x aus I:
eine (n+1)-mal stetig differenzierbare Funktion. Dann gilt für alle a und x aus I:
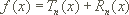
mit dem n-ten Taylorpolynom an der Entwicklungsstelle a
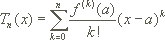
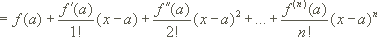
und dem n-ten Restglied
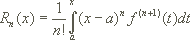
In den Formeln stehen 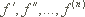 für die erste, zweite, ... n-te Ableitung der Funktion f.
für die erste, zweite, ... n-te Ableitung der Funktion f.
2. Beweis
Der Beweis dieser Formel für das Restglied erfolgt durch Induktion, der Induktionsanfang n=0 entspricht dabei genau dem Fundamentalsatz der Analysis:
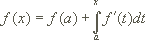
Der Induktionsschritt 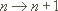 erfolgt durch partielle Integration (es ist zu zeigen, dass die Formel für n+1 gilt):
erfolgt durch partielle Integration (es ist zu zeigen, dass die Formel für n+1 gilt):
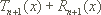
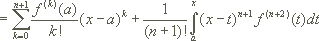
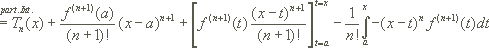
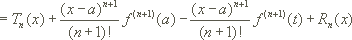
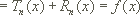
3. Restgliedformeln
Es gibt außer der Integralformel noch andere Darstellungen des Restgliedes. Eine ist die Lagrangesche Form des Restgliedes:
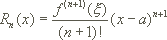
für ein  zwischen a und x.
zwischen a und x.
Sie ist der Spezialfall p=n+1 der Schlömilch'schen Restgliedform für die natürliche Zahl p mit  :
:
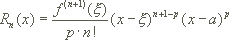
für ein  zwischen a und x.
zwischen a und x.
Im Spezialfall p=1 erhalten wir das Cauchy'sche Restglied:
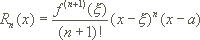
für ein  zwischen a und x.
zwischen a und x.
Das Restglied hat die Eigenschaft, für x gegen a schnell gegen 0 zu konvergieren, genauer gilt:
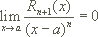
Das bedeutet, je näher x bei a liegt, desto besser stimmt das Taylorpolynom Tn an der Stelle x mit der Funktion f überein.
4. Näherungsformeln für Sinus und Kosinus
Eine Anwendung der Taylorformel sind Näherungsformeln, hier vorgestellt für Sinus und Kosinus (wobei das Argument im Bogenmaß angegeben wird).
Das 3. Taylorpolynom T3,sin der Sinusfunktion an der Entwicklungsstelle 0 hat diese Gestalt:
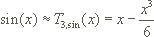
Liegt x zwischen - /4 und
/4 und  /4, dann liegt die relative Abweichung |(T3,sin(x)-sin(x))/sin(x)| bei unter 0,5%.
/4, dann liegt die relative Abweichung |(T3,sin(x)-sin(x))/sin(x)| bei unter 0,5%.
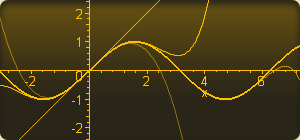
Die folgende Abbildung zeigt die Graphen einiger Taylorpolynome Tn des Sinus für n=1, 3, 5, 15. Der Graph zu n= gehört zur Taylorreihe, die mit der Sinusfunktion übereinstimmt.
gehört zur Taylorreihe, die mit der Sinusfunktion übereinstimmt.
Das vierte Taylorpolynom T4,cos der Kosinusfunktion an der Entwicklungsstelle 0 hat im Horner-Schema diese Gestalt:
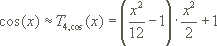
Liegt x zwischen - /4 und
/4 und  /4, dann liegt die relative Abweichung |(T4,cos(x)-cos(x))/cos(x)| bei unter 0,05%.
/4, dann liegt die relative Abweichung |(T4,cos(x)-cos(x))/cos(x)| bei unter 0,05%.
Will man mit diesen Näherungsformeln den Sinus oder Kosinus von anderen x-Werten berechnen, sollte man die Reduktionsformeln benutzen, um |x| kleiner als  /4 zu machen.
/4 zu machen.
Auch für Tangens und Kotangens kann man diese Formeln nutzen, denn es ist
tan(x) ~ t(x) = T3,sin(x) / T4,cos(x)
mit einer relativen Abweichung von unter 0,5% für |x| <  /4, und cot(x) ~ 1/t(x) mit derselben relativen Abweichung. (Dabei ist t kein Taylorpolynom des Tangens.)
/4, und cot(x) ~ 1/t(x) mit derselben relativen Abweichung. (Dabei ist t kein Taylorpolynom des Tangens.)
Braucht man eine noch höhere Genauigkeit für seine Näherungsformeln, dann kann man auf höhere Taylorpolynome zurückgreifen, die die Funktionen noch besser approximieren. Warum das so ist, wird im Artikel Taylorreihe erläutert.
5. Taylor-Formel im Mehrdimensionalen
Sei 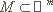 offen,
offen, 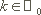 und
und 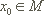 .
.
Die Funktion 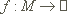 sei (k+1)-mal stetig differenzierbar, also aus Ck+i(M).
sei (k+1)-mal stetig differenzierbar, also aus Ck+i(M).
Dann gibt es für alle 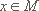 mit
mit 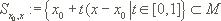 ein
ein 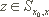 mit
mit
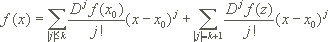
wobei j ein Multiindex ist mit:
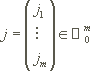
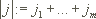 heißt die Länge von j
heißt die Länge von j
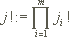
und 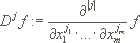
aus Wikipedia, der freien Enzyklopädie